【译】用Java构建简单的神经网络

本篇文章翻译自一篇英文博客，加入了自己的一些理解，力求通俗易懂，向非专业人士科普神经网络，如有不足之处欢迎在评论区提出宝贵意见，阅读原文请戳原文链接

在这篇文章中我们将使用简单的步骤来解决人工智能问题，并且尝试使用Java来构建一个简单的神经网络。

什么是神经网络？

神经网络是一种模拟大脑如何工作的数学模型。遗憾的是，我们还不知道大脑到底是如何工作的，但是我们确实知道一些背后的生物学原理：人类的大脑包含大约一千亿个神经元，它们被突触连接在一起，如果连接到神经元的突触被激活，那么神经元也会被激活。这个过程被称为“思考”。

因此我们尝试使用一个简单的案例来对上述过程进行建模，这个案例包含三个输入和一个输出。三个输入通过三个突触连接到一个神经元上，神经元激活后产生一个输出。

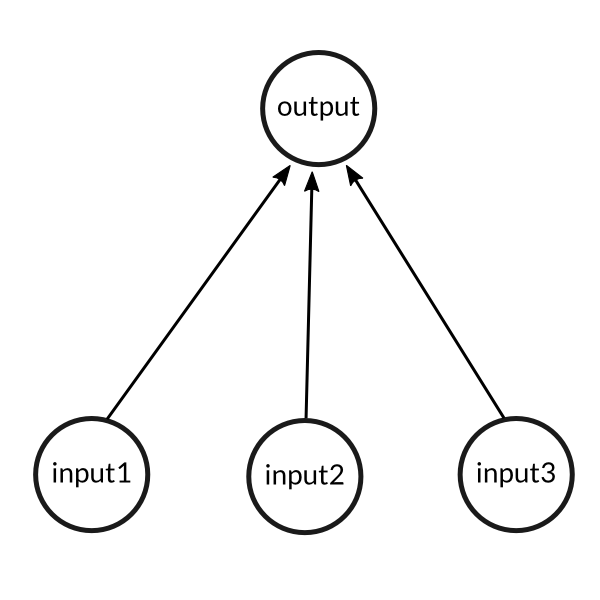
一个简单的问题

我们将训练上述神经网络来解决以下问题。你能找出其中隐含的规律并且猜出新的输入对应的输出是什么吗？0还是1？

数据	输入1	输入2	输入3	输出
数据1	0	0	1	0
数据2	1	1	1	1
数据3	1	0	1	1
数据4	0	1	1	0
新数据	1	1	0	?

答案实际上就是最左边一列的值，即1！

训练过程

所以现在我们有一个人脑模型，我们将尝试让我们的神经网络去学习给定训练集（即所有用于学习的数据，每条数据包含三个输入和一个输出）中的规律。我们将首先赋予每个输入一个随机数字（即每个输入对应的权重）来产生一个输出。

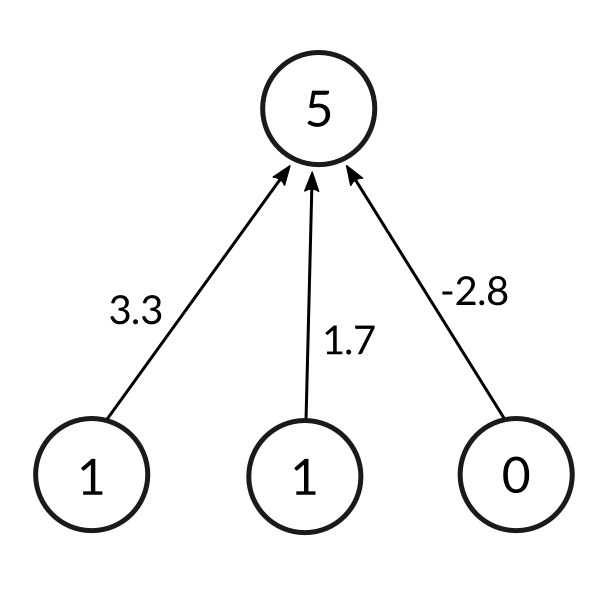
计算输出的公式如下：

$$\sum weight_i . input_i = weight1 . input1 + weight2 . input2 + weight3 . input3$$

现实中我们希望将输出值转化为0到1之间的某个数，使预测结果有意义，这个过程被称为“归一化”。我们将归一化后的输出与我们期望的输出（即训练集中的输出）作对比，这将产生错误，或者称之为与期望值之间的差距（即误差）。然后，我们可以根据错误对神经网络的权重进行微调，并且再次在同样的数据上进行尝试。这个过程可以总结成下面这张图：

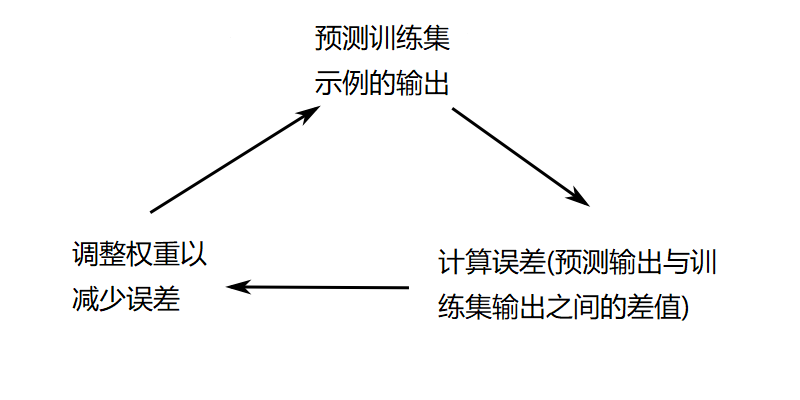
我们对所有数据（所有数据在每轮中计算一次误差）重复这样的训练过程10,000次，让神经网络获得充分训练。接下来我们可以使用这个神经网络对新的输入进行预测。

但是，在进行具体实现之前，我们仍然需要弄清楚归一化的过程是怎样的，以及如何根据错误来调整每个输入权重（也称之为反向传播）。

归一化

在受生物学启发的神经网络中，一个神经元的输出通常代表着细胞中动作电位的触发。其最简单的形式为一个二进制数，即神经元是否被触发。因此，需要对输出值进行归一化。

为了实现这种归一化，我们将一个函数应用于神经元的输出，该函数被称为“激活函数”。如果我们把简单的跃阶函数（即将负数转化为0，正数转化为1）作为激活函数，则需要大量神经元来达到缓慢调整权重减少误差的目的，原因在于该函数输出非0即1，粒度太粗。

我们将在下一部分有关反向传播的内容中讲到，“缓慢调整权重”这一概念与数学语言中激活函数的斜率有关。从生物学的角度来说就是随着输入电流的增加，激活的速度就越快。如果我们使用线性函数而不是跃阶函数，那么我们会发现，由于线性函数的输出并不在0和1之间，因此在缓慢调整权重的过程中神经元的输出将趋于无限制地增加，因此最终的网络将具有不稳定的收敛性。

上面提到的所有问题都可以通过使用可归一化的S型激活函数来解决。可以类比现实中这样一个近似的模型，变量一开始保持为零，一旦接收到电流，开始迅速增加，并逐渐接近100％。从数学上讲，对应这样一个式子：

$$\frac{1}{1 + e^{-x}}$$

如果在图表上绘制，可以得到一条S型曲线：

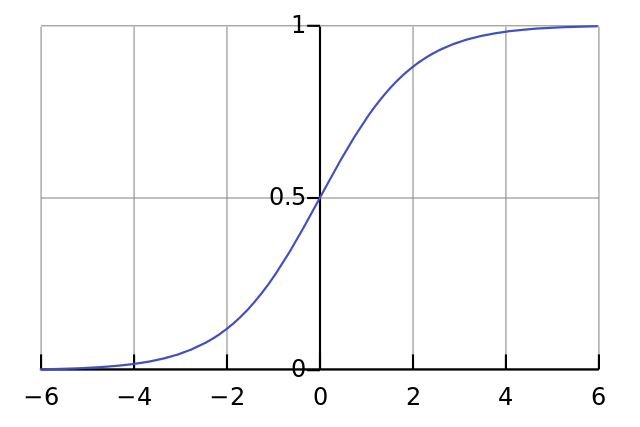
因此，神经元输出的最终公式变为

$$Output = \frac{1}{1 + e^{-(\sum weight_i . input_i)}}$$

我们还可以使用其他归一化函数，但S型曲线的优点是非常简单，并且具有简单的导数，这将非常有利于我们接下来要讲的反向传播。

反向传播

在每轮的训练中，我们根据错误调整权重。为了做到这一点，我们引入“调整公式”

$$Adjustment = error . input . SigmoidCurveGradient(output)$$

我们使用这个公式的首要原因是我们需要根据误差的大小来调整权重。其次，我们将调整后的权重与输入（要么是0要么是1）相乘，所以调整与输入也有关，如果输入是0，则权重等于没有调整。最后，我们还要乘上S型曲线的梯度（或者称之为导数）。

为什么与梯度有关呢？因为我们要将错误最小化，即让神经网络尽可能少犯错。具体来说，可以通过梯度下降方法来做到这一点。即从参数空间中的当前点开始（当前点由当前所有参数的权重确定），每次都朝着错误减小的方向调整。形象化的描述就是，站在山坡上并沿着坡度最陡的方向走。应用于神经网络的梯度下降方法如下所示：

如果神经元的输出是一个较大的正数或负数，则表明该神经元非常倾向于认为结果是1或者是0。
从S型曲线图中可以看出，此时曲线的斜率较小。
因此，如果神经元确信当前的权重是正确的，那么它就不需要调整太多，而乘以S型曲线的斜率就可以实现这一点。

S型函数的导数由下面的公式给出

$$SigmoidCurveGradient(output) = output . (1 - output)$$

将其代入调整公式可得到

$$Adjustment = error . input . output . (1 - output)$$

代码

在解释以上数学概念时，遗漏了重要但微妙的一点，对于每次训练迭代，数学运算都在整个训练集上同时完成。因此，我们将利用矩阵来分别存储输入向量，权重和预期输出的集合。

你可以在此处获取整个项目的源代码：https://github.com/wheresvic/neuralnet 。为了方便学习，我们仅使用标准的Java Math函数自己实现了所有数学运算：)

我们将从NeuronLayer类开始，该类只是神经网络实现中的权重部分。我们为它提供每个神经元的输入数量以及可用于构建权重表的神经元数量。在我们当前的示例中，这只是具有3个输入神经元的最后一个输出神经元。

public class NeuronLayer {

    public final Function activationFunction, activationFunctionDerivative;

    double[][] weights;

    public NeuronLayer(int numberOfNeurons, int numberOfInputsPerNeuron) {
        weights = new double[numberOfInputsPerNeuron][numberOfNeurons];

        for (int i = 0; i < numberOfInputsPerNeuron; ++i) {
            for (int j = 0; j < numberOfNeurons; ++j) {
                weights[i][j] = (2 * Math.random()) - 1; // 把范围从O~1调整为-1~1
            }
        }

        activationFunction = NNMath::sigmoid;
        activationFunctionDerivative = NNMath::sigmoidDerivative;
    }

    public void adjustWeights(double[][] adjustment) {
        this.weights = NNMath.matrixAdd(weights, adjustment);
    }
}

我们的神经网络类是所有动作发生的地方。它以NeuronLayer作为构造函数，并具有2个主要功能：

think：计算给定输入集的输出
train：运行训练循环numberOfTrainingIterations次（通常是10,000这个级别的数字）。请注意，训练本身涉及计算输出，然后相应地调整权重

public class NeuralNetSimple {

    private final NeuronLayer layer1;
    private double[][] outputLayer1;

    public NeuralNetSimple(NeuronLayer layer1) {
        this.layer1 = layer1;
    }

    public void think(double[][] inputs) {
        outputLayer1 = apply(matrixMultiply(inputs, layer1.weights), layer1.activationFunction);
    }

    public void train(double[][] inputs, double[][] outputs, int numberOfTrainingIterations) {
        for (int i = 0; i < numberOfTrainingIterations; ++i) {

            // 将训练集中的数据通过网络进行传播
            think(inputs);

            // 通过 error * input * output * (1 - output) 调整权重

            double[][] errorLayer1 = matrixSubtract(outputs, outputLayer1);
            double[][] deltaLayer1 = scalarMultiply(errorLayer1, apply(outputLayer1, layer1.activationFunctionDerivative));

            // 计算要调整多少
            double[][] adjustmentLayer1 = matrixMultiply(matrixTranspose(inputs), deltaLayer1);

            // 调整权重
            this.layer1.adjustWeights(adjustmentLayer1);
        }
    }

    public double[][] getOutput() {
        return outputLayer1;
    }
}

最终，我们有了main方法来设置训练数据，训练网络并要求其对测试数据进行预测

public class LearnFirstColumnSimple {

    public static void main(String args[]) {

        // 创建包含一个神经元和三个输入的隐含层（神经网络中除去输入层和输出层，其他层被称为隐含层）
        NeuronLayer layer1 = new NeuronLayer(1, 3);

        NeuralNetSimple net = new NeuralNetSimple(layer1);

        // 训练网络
        double[][] inputs = new double[][]{
                {0, 0, 1},
                {1, 1, 1},
                {1, 0, 1},
                {0, 1, 1}
        };

        double[][] outputs = new double[][]{
                {0},
                {1},
                {1},
                {0}
        };

        System.out.println("Training the neural net...");
        net.train(inputs, outputs, 10000);
        System.out.println("Finished training");

        System.out.println("Layer 1 weights");
        System.out.println(layer1);

        // 计算对新数据的预测结果

        // 1, 0, 0
        predict(new double[][], net);

        // 0, 1, 0
        predict(new double[][], net);

        // 1, 1, 0
        predict(new double[][], net);
    }

    public static void predict(double[][] testInput, NeuralNetSimple net) {
        net.think(testInput);

        // 打印结果
        System.out.println("Prediction on data "
                + testInput[0][0] + " "
                + testInput[0][1] + " "
                + testInput[0][2] + " -> "
                + net.getOutput()[0][0] + ", expected -> " + testInput[0][0]);
    }
}

运行上面的示例，我们看到网络在预测最左边的输入为1的时候做得很好，但是为0的时候得到正确结果的概率似乎较低！这是因为训练结果中第二和第三输入权重都需要都接近0。

Training the neural net...
Finished training
Layer 1 weights
[[9.672988220005456 ]
[-0.2089781536334558 ]
[-4.628957430141331 ]
]

Prediction on data 1.0 0.0 0.0 -> 0.9999370425325528, expected -> 1.0
Prediction on data 0.0 1.0 0.0 -> 0.4479447696095623, expected -> 0.0
Prediction on data 1.0 1.0 0.0 -> 0.9999224112145153, expected -> 1.0

在下一篇文章中，我们将看到在神经网络中额外添加一层是否有助于改善预测；）

参考资料

Milo Spencer-Harper的教程，介绍如何使用python创建简单的神经网络。
Steven Miller撰写的有关构建简单神经网络的教程。
维基百科有关激活函数的文章